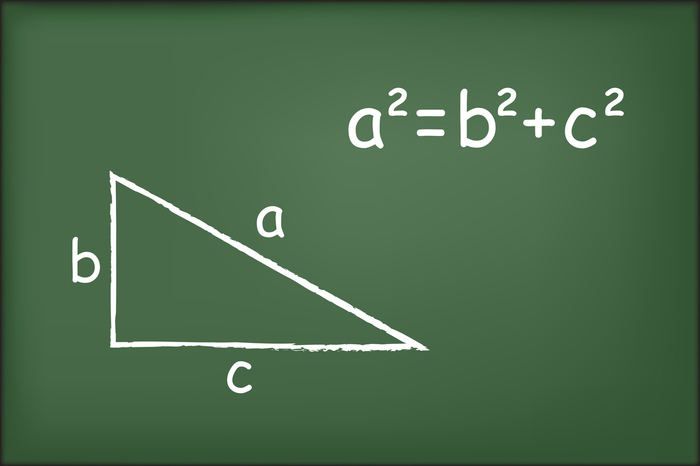Antes de falar sobre o famoso Teorema de Pitágoras, há algumas coisas a lembrar sobre triângulos …
PREMISSA
Entre todos triângulos na verdade, um tem muitas propriedades úteis e interessantes: Triângulo retângulo.
Um triângulo retângulo tem um ângulo reto: ou seja, tem a forma de um Esquadro.

Na verdade, existem dois quadrados de desenho no mercado: o de cima e o de dois lados iguais.
Por outro lado, existem muitos triângulos retângulos: um para cada ângulo agudo. Por exemplo, podemos querer imaginar um triângulo retângulo com um lado de um centímetro e o outro indo daqui … para a lua. Este triângulo longiiiiiiiiiiiiiiiiiiissimo também é um retângulo.
Bem, todos os triângulos retângulos têm uma propriedade muito simples e muito útil e é o Teorema de Pitágoras.
Leia também: O Teorema de Pitágoras foi realmente provado por Pitágoras?
TEOREMA
Para descobrir do que se trata, convido você a montar um quebra-cabeça com uma tesoura, uma régua e um papelão. Siga-me passo a passo.
- Recortado um triângulo retângulo.
- Coloque-o sobre o papelão e recorte. uma cópia idêntica.
- Repita até que você tenha oito triângulos retângulos de qualquer maneira: se você os sobrepuser, obterá uma pilha perfeita, sem ninguém se destacar dos outros.
- Medir o três lados do triângulo retângulo (os curtos são chamados de catheti, os longos são chamados de hipotenusa).
- Agora corte três quadrados: o primeiro com o lado igual a uma perna, o segundo com o lado igual a outra perna, e o terceiro com o lado igual à hipotenusa.
Excelente! Você tem na sua frente onze figuras: oito triângulos retângulos, todos iguais entre si, e três quadrados cada um com o lado igual a um dos lados dos triângulos.
Pegue o quadrado “Construído na hipotenusa” e quatro triângulos. Tenho certeza que você pode colocá-los lado a lado para formar este quadrado.
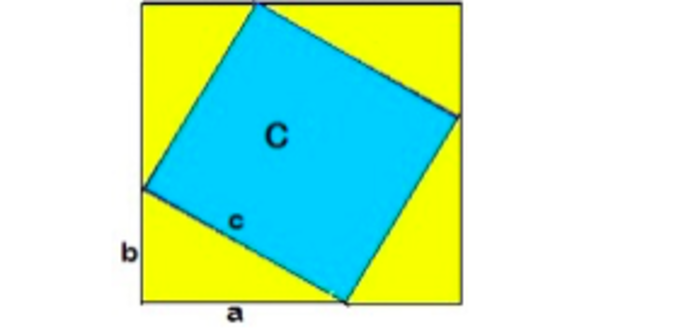
Qual é o tamanho do seu lado? Bem, vemos que seu lado é dado pelas duas pernas: é a soma deles.
Agora pegue os dois quadrados e os outros quatro triângulos e forme este quadrado.
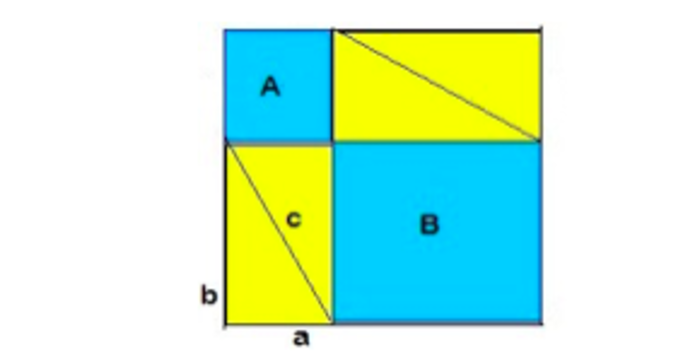
Se eles perguntassem novamente quanto é o lado dele, você diria enquanto avança que o lado dele é a soma das pernas.
Os dois quadrados são iguais: eles se sobrepõem exatamente. Ver é crer.
Mas … por que devemos estar interessados nisso? Porque se você remover os triângulos de ambas as figuras, eles permanecem de um lado a praça construída na hipotenusa, no outro os quadrados construídos nas pernas.